
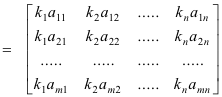
Where we have used the fact that the determinant of L is 1. Taking the determinant of both sides yields Where L is lower triangular with 1s on the main diagonal, U is upper triangular, and P is a row-permutation matrix. Note that the determinant of a product of matrices is the product of the determinants. The determinant is calculated via the LU decomposition. In any case, the syntax for its use is y = det(A) The condition number cond gives a more reasonable estimate as to the suitability of a matrix for inversion than comparing det(A) to zero. Note that for all but very small problems, the determinant is not particularly useful. We do Step 6 to find out which eigenvalue will replace λ 1, λ 2, and λ 3 in the initial diagonal matrix created in Step 1.Section: Array Generation and ManipulationsĬalculates the determinant of a matrix. Step 6: Finding P -1 and then putting values in diagonalization of a matrix equation.

Step 3: Find the eigen vectors X 1, X 2, X 3 corresponding to the eigen values λ = 1,2,3. Problem Statement: Assume a 3×3 square matrix A having the following values:įind the diagonal matrix D of A using the diagonalization of the matrix. Step 5: Find P -1 and then use the equation given below to find diagonal matrix D. Here, all the eigenvectors till X i have filled column-wise in matrix P. Step 3: Compute the corresponding eigen vectors using the equation given below. Owner: TJ Cyders Labels: None Priority: 5 Updated: Created: Creator. Formatting Help 200 trace - sum of diagonal elements Status: closed. Changes Closed Tickets Open Tickets Help. Now zero the subdiagonal elements that have just been introduced, and apply. Step 2: Find the eigen values using the equation given below. FreeMat Feature Requests Brought to you by: dkyriakis, geneing, samitbasu. Updates the upper triangular (lower left 0) matrix Rf PXQ. Step 1: Initialize the diagonal matrix D as: In simpler words, it is the process of taking a square matrix and converting it into a special type of matrix called a diagonal matrix. Flow controls and conditional statements: if comparison structure, switch comparison structure. Polynomials and solutions of linear systems.
#FREEMAT DIAGONAL OF MATRIX HOW TO#
It is generally used in the process of diagonalization and similarity transformation. Matrices: how to create a matrix, square and rectangular matrices, identity and diagonal matrices, operations with matrices and access to the elements of a matrix. Modal matrix: It is a (n x n) matrix that consists of eigen-vectors. As per the similarity transformation, if the matrix A is related to D, thenĪnd the matrix A is reduced to the diagonal matrix D through another matrix P. B can be considered similar to A if there exists an invertible matrix P such that B=P^ A P This is known as Matrix Similarity Transformation.ĭiagonalization of a matrix is defined as the process of reducing any matrix A into its diagonal form D.
ML | One Hot Encoding to treat Categorical data parameters.ML | Label Encoding of datasets in Python.The most elegant alternative, however, is to use ReplacePart a little more effectively: the replacement Rule can be a RuleDelayed, e.g. Introduction to Hill Climbing | Artificial Intelligence DiagonalMatrix also accepts a second integer parameter which allows you to specify which diagonal that newDiagList represents with the main diagonal represented by 0.Best Python libraries for Machine Learning.Activation functions in Neural Networks.Elbow Method for optimal value of k in KMeans.Decision Tree Introduction with example.
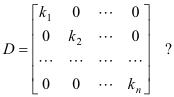
Linear Regression (Python Implementation).Removing stop words with NLTK in Python.ISRO CS Syllabus for Scientist/Engineer Exam.ISRO CS Original Papers and Official Keys.GATE CS Original Papers and Official Keys.


 0 kommentar(er)
0 kommentar(er)
